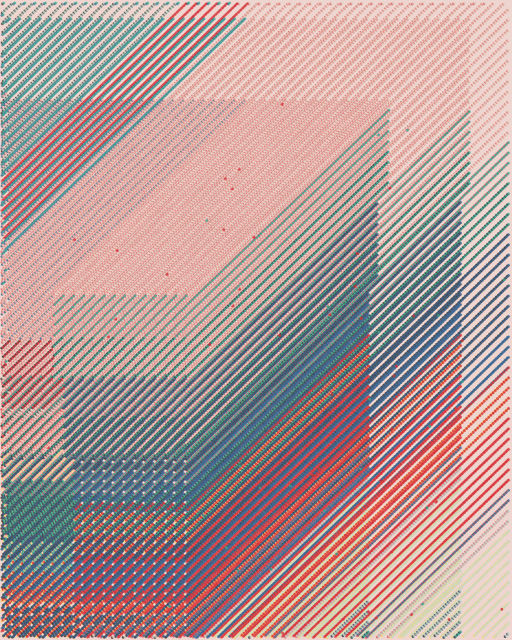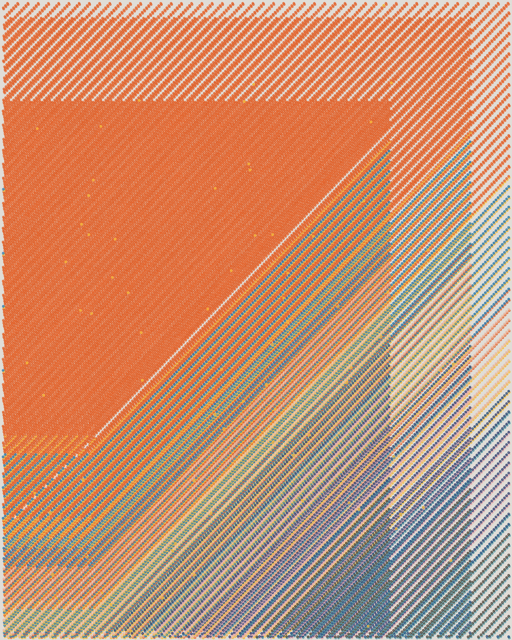Musical scores
QQL seeds often feel like music. When I discovered the seed that would become QQL #274, I immediately saw its connection to Maurice Ravel's Boléro. The likeness to Boléro with the seed's rhytmic structure together with its crescendo was an obvious comparison.
For "Musical scores" I wanted to liken the repeating structure of horizontal-direction QQLs to that of sheet music. Rings looking like notes, often running smoothly but also full of life and with tone-changes that add expression and life to the composition.
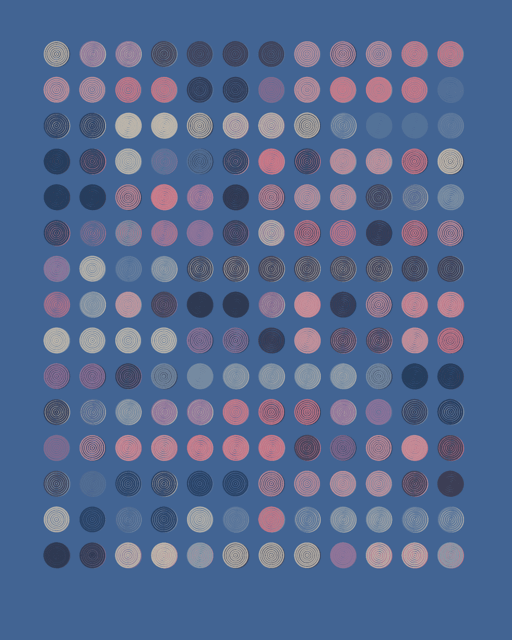
QQL palette grid
A "common" grid of 180 rings in all palettes and many backgrounds. 7-ring-dot, think, medium, sparse & constant rings on the larger side of medium with a wide margin. Vertical formation without turbulence. Stacked, high color variance. The ring position in this grid of 180 seems to be fixed with a slightly larger margin on the right and bottom sides.
QQL trio: Order/Disorder
In November 2024, the Museum of Art and Light opens its doors with "Code & Canvas", a 5-month long exhibition featuring Tyler Hobbs and 4 other notorious digital artists. Tyler's exhibit will showcase QQL with a focus on co-creation as a key element of the artwork. There will be a trio of QQLs in display that will feature 2/6 seeds curated by Tyler + 1 seed & the trio composition curated by a community member and selected by Tyler in competition. Below, Tyler Hobb's 6 seeds.
All 6 seeds share the same traits: Fidenza, simple-high variety color, low turbulence formation, with medium rings, a crips margin and a healthy mix of thin and thick rings. Although they have the random radial trait, when curvature shows up it does so timidly. Intangibly, but indispensably at the center of the trio to be, we find one of Tyler Hobb's core art concepts, the balance of order and disorder that the emergent nature of complex algorithms deliver.
While the first 3 seeds have a complex structure with multiple sectors of with rings of slightly different sizes and varying compositions, the latter 3 are simpler, with monosectorial distribution each of them paired with a distinctive accent area. Otoh, while these seeds may appear as unconsequential at first sight, all of them are full of life and small details to discover upon further inspection.
I took all the above ideas and observation into account when pairing one of my own seeds with 2 of Tyler's. (opinion) To compose a succesfull trio, the 3rd seed needs to complement the other 2 in most if not all ways. When the 3rd seed contrasts with the other 2, coherence of the whole needs to be maintained otherwise harmony breaks and the trio becomes unsuccesful.
QQL #14. One and only?
Selected by Emily Xie for day 0 contest, found and minted by RobotChicken and finally collected by QQL creator Indigo, #14 is one of the most captivating QQLs ever minted. The only conceptually similar QQL in the whole collection is #296 which took Von Misses & Xatarrer months of curation and +100M seeds to find.
What makes #14 so special, you ask? A seed made of an identifiable 3x3 grid. Each section has a unique ring pattern but they dialogue between each other and all converge at the top. Color variety is sustained and gives balance and sense to the composition. There's just enough white space. And the red upwards tornado together with the 3 larger white rings are front and center taking the spotlight.
Like Xatarrer before me, I took on the (impossible?) task to find a seed that had a similar stunning result. It took me a while to discover that seeds with sector grids larger than 3x3 where all too busy for a distinct subtle composition to emerge. In seeds with more than 5 or 6 colors, composition becomes diluted. Thinning flow fields appear scarcily and almost never with all smaller ring sectors flowing all towards the edge to create a nice background to the seed. Getting distinctive sectors across the canvas is no common feat either. While Fidenza is the other palette that can result in a balanced contrast between white, red and blue, it felt that for the sake of constance, a successor seed had to be found in Edinburgh.
Below are 16 seeds that although don't get as near the goal as I would have hoped, are at the very least close to #14.
Berlin Gold
There are 33 backgrounds and 120 ring colors in QQL. Each of these colors can present itself with a variance of +2/-2 in hue, saturation and brightness which gives QQL seeds a very interesting and almost imperceptible texture of varying lightness that gives just so much depth to the artwork.
To me, one of the most striking colors in the collection is "Berlin Dim Orange", aka "Berlin Gold" which, with its characteristic brightness, works beautifully in contrast with the dimmer tones present in the Berlin palette. Specially, when combined in staked mode with other color rings, it generates a shiny effect in yet so many more tones.
To highlight this extraordinary variety of color in QQL, as well as the stunning presence that "Berlin Dim Orange" gives, I proposed "Berlin Gold" as a QQL Monthly theme. Below we can discover some of my favorite community seeds this theme.
Diagonal Recursion
Thinning paralel lines of rings, with rhitmically diminishing density towards one of the corners of the canvas, often forming elongated triangles, that slowly let the background color come through.
This elegant rhythm is what gives these QQL seeds a timeless elegance, a simple yet balanced composition that's often hard to find.
It feels almost impossible, that this style of elusive seed was discovered so early in QQL history, for it was Andrew Jiang from Curated who presented the seed that would become QQL #3, the first recursive QQL, that was to be selected by Sofia Garcia for the Day 0 contest.
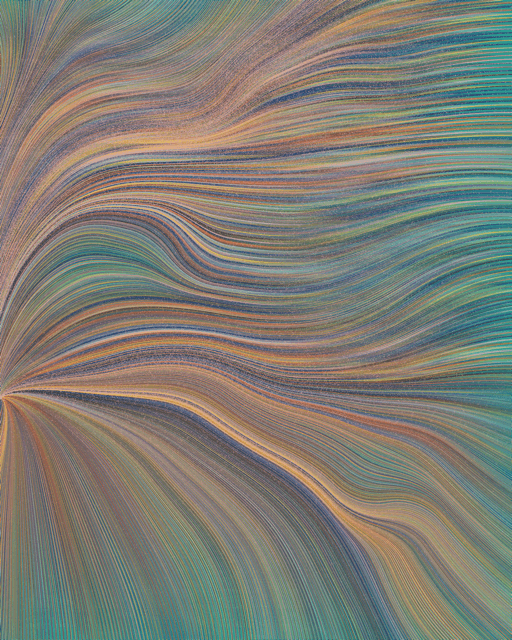
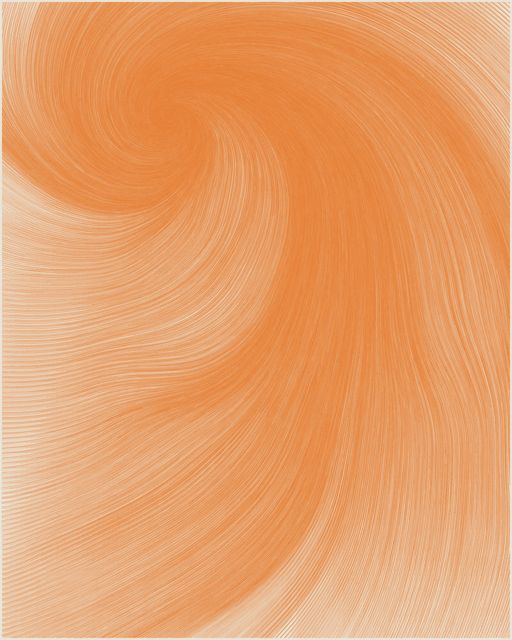
Focus on Me
Focus on me, look into the eye of the seed.
For a moment, forget everything else.
Right now it's just you and the vortex of the flow field.
Loose yourself in the spiraling paths of ever-smaller rings.
Close your eyes.
Breath in through your nose. Pause for a moment.
And, slowly, let the air out through your mouth.
As you exhale, notice how a deep sense of relaxation fills your whole body.
Open your eyes.
Now, go back into the woods.
WYSIWYF. What You See Is What You Feel.
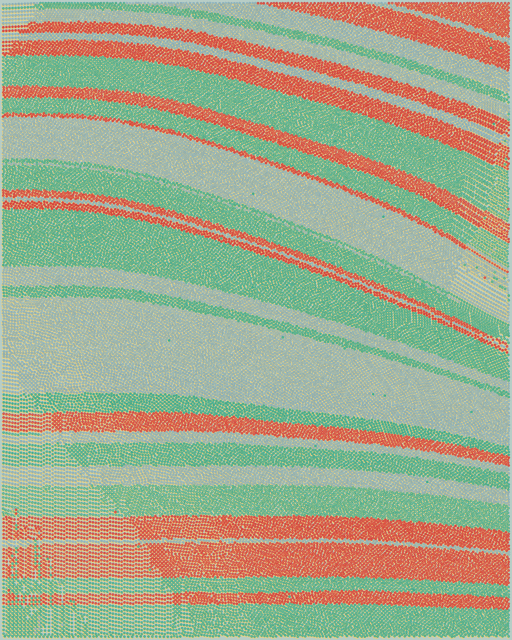
Meridian
Meridian by Matt Deslauriers has become one of the most timeless collections of the long-form generative art movement. A collection of intertconnected landscapes made of wavy stratified pointillist color bands.
It's precisely this stratification where we can find the connection between QQL and Meridian. So much so, that "Meridian" has even become a substyle within Tyler and Indigo's artwork. It's in a way testament, once more, to the vast diversity that the QQL algorithm hides within its apparent randomness. While Meridian stratum often present a hilly shape, QQl's potential tends to be flat or wavy, but both share a somewhat recurrent intercalation of color.
All Meridian-like QQLs presented were found in Fidenza palette.
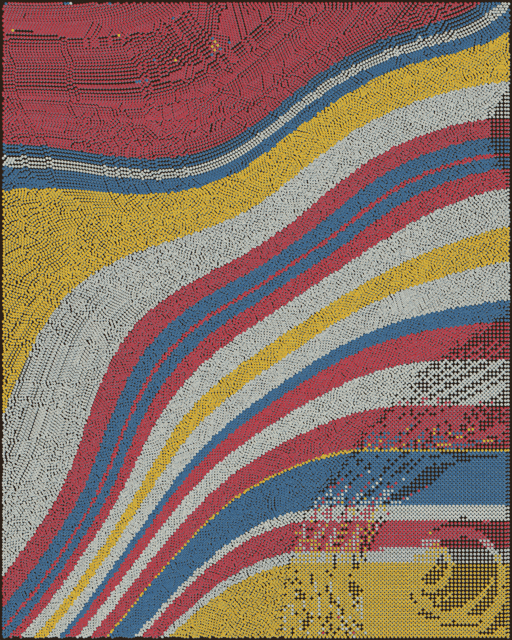
QQL #268, one of each
One of my favorite QQL's I found on Year 1 was QQL #268. It's a zig-zagging compendium of constant medium rings that seems to want to create a Zebra composition of all possible Miami color combinations. It has this simplicity, structure and regularity that I find so attractive.
While most QQL structures are impossible to replicate, certain ones seem to be at the formal edges of the algorithm and #268 is one of them. That's why I spent a month generating seeds in all 7 palettes to find QQLs that had the same quantity of rings position in the same way as the original one.
One Ring
The ring, QQL's nuclear element from which all compositions arise. Only when looking at single rings can we trully understand the sheer variability of the algorithm. We can commonly find rings in 1, 3 & 7 sub-rings and with a bit more knowledge/luck in 2, 4, 5 & 6 sub-rings as well.
When we take into account that these rings have variable thickness and can appear each in one of QQLs 153 colors, that these colors may have slight deviations, that each palette has several different backgrounds (within these colors) and that when the color mode is Stacked or Zebra yet another color enters the equation of ring variations, possibilities seem endless.
When focusing on one ring as the key element we also have to take into account its size and the position it takes in the canvas. Central rings are quite an oddity within the algorithm (my occurrence, under ideal conditions, is of around 0.1%) and some good examples would be #55, #109 & #253
Below, the results of a month of searching for QQL seeds with 1 single central ring through all palettes and modes.
Inflated
Every so often, when rendering a batch, a blank QQL seed will generate. Most of the times, these seeds have millions of "secret" negative-radius rings that can't display.
Thanks to wchargin's QQL renderer, a Rust implementation of the algorithm that's full of neat features, we can now see all these invisible rings with a minimum-visible-radius that brings them to life and shows a hidden side of QQL that gives us not what is, but what could have been.
These below are the inflated version of mostly-blank QQL seeds.